算法小结之动态规划

发表于 分类于 阅读次数： 本文字数： 4.3k 阅读时长 ≈ 4 分钟

前言

在上篇讨论 递归 的文章中，最后留了一道八皇后的问题，我们很自然的可以想到一种思路：顺着棋盘的每一行或每一列，我们找到一个可以放置皇后的位置，连续找到 8 个位置就是一组解。

但和之前的三道递归问题有着明显的不同，每一次放置的棋子，不仅依赖于之前放置的棋子，同时也会影响剩下来的棋子，而且每次可以放置的位置并不都唯一。

八皇后

问题描述

在 8×8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

解题思路

按照前言中的思路，定义棋盘 bool[,] chessboard ，我们尝试一下：

  1. 先定义一个方法 bool SetQueens(bool[,] chessboard, int row)， 这个方法表示在第 row 行，放置一个皇后，如果找不到可以放置皇后的位置，则方法返回 False

  2. 对于每一行而言，每一个格子都需要尝试放置皇后，我们再定义一个方法 bool CheckValid(bool[,] chessboard, int row, int col) 用来判断在 row 行 col 列放置的皇后是否合法

  3. 如果找到一个合法位置，那么很显然我们要做的事情就是在下一行继续尝试放置皇后，同时，因为我们是在每一行的所有格子都要做一遍测试，所以在这一行的下一次尝试之前，我们需要取回这一次在这一行放置的棋子

    1
    2
    3
    4
    5
    6
    7
    8
    9
    for (int col = 0; col < chessboard.GetLength(1); col++)
    {
        chessboard[row, col] = true;//放置皇后
        if (CheckValid(chessboard, row, col))
        {
            SetQueens(chessboard, row + 1);//放置合法，到下一行放置皇后
        }
        chessboard[row, col] = false;//取回皇后，避免干扰同一行的下一次尝试
    }

  4. 不停的尝试下一行，直到放完所有行的时候，我们就得到了一个可行的解法

    1
    2
    3
    4
    if (row == chessboard.GetLength(0))
    {
        Result.Add((bool[,])chessboard.Clone());
    }

整合一下，bool SetQueens(bool[,] chessboard, int row) 的方法体就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void SetQueens(bool[,] chessboard, int row = 0)
{
    if (row == chessboard.GetLength(0))
    {
        //到这里，chessboard的状态就是一组可行解
        return;
    }
    for (int col = 0; col < chessboard.GetLength(1); col++)
    {
        chessboard[row, col] = true;
        if (CheckValid(chessboard, row, col))
        {
            SetQueens(chessboard, row + 1);
        }
        chessboard[row, col] = false;
    }
}

当然，之前我们定义了 bool CheckValid(bool[,] chessboard, int row, int col)，根据规则很容易理解就是横竖撇捺上不能有其他棋子。

  • 横：由于我们是一行一行放置的，所以横一定是唯一的，就不用判断了；
  • 竖：把这一列遍历一次，做判断；
  • 撇：斜率为 1 且经过 (row, col) 这个点的直线，在正方形内的整数坐标，做判断；
  • 捺：斜率为 -1 且经过 (row, col) 这个点的直线，在正方形内的整数坐标，做判断；

根据这个思路，很容易写出方法体了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool CheckValid(bool[,] chessboard, int row, int col)
{
    for (int i = 0, j; i < chessboard.GetLength(0); i++)
    {
        if (i != row && chessboard[i, col])//竖
        {
            return false;
        }
        j = i + col - row;//撇：斜率为1
        if (j >= 0 && j < chessboard.GetLength(1) && j != col && chessboard[i, j])
        {
            return false;
        }
        j = col + row - i;//捺：斜率为-1
        if (j >= 0 && j < chessboard.GetLength(1) && j != col && chessboard[i, j])
        {
            return false;
        }
    }
    return true;
}

问题小结

代码：HT.Algorithm的 EightQueens

在这里不考虑对称的问题，八皇后有 92 组解。

八皇后这个问题在网上很容易找到许多简短的算法，像用一维数组做记录、位运算之类的，但本质上都是需要回溯的，其他算法的精妙之处在这里按下不表。

双蛋问题（鸡蛋掉落、鹰蛋问题）

为了能够自然的引入这个问题，又写递归，又写八皇后的，都感觉有点买椟还珠了。😂

其实是看了李永乐老师的一个视频，复工复产找工作？先来看看这道面试题：双蛋问题，想记录一下解答过程。

问题描述

问题大意：蛋在某层楼以下扔都不会碎，有 T 层楼，N 个蛋，在运气最差的情况下，找到临界楼层需至少要 M 次，求 M 的值。

定义 M(T,N) 表示这个答案。

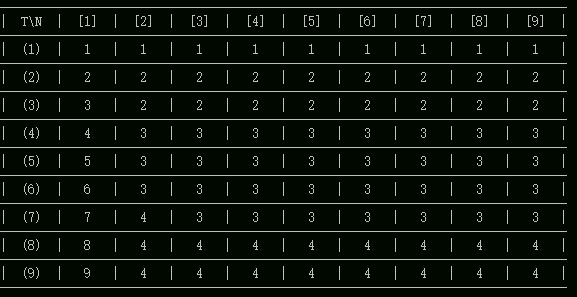
视频中 11 分钟的表格我照抄一份：

T\N 1 2 3 4 5 6 7 8 9
1 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2
3 3 2 2 2 2 2 2 2 2
4 4 3 3 3 3 3 3 3 3
5 5 3 3 3 3 3 3 3 3
6 6 3 3 3 3 3 3 3 3
7 7 4 3 3 3 3 3 3 3
8 8 4 4 4 4 4 4 4 4
9 9 4 4 4 4 4 4 4 4

解题思路

在 T 层楼中选择第 k 层扔蛋：

  1. 如果碎了，在 (1, k - 1) 之间，找出临界楼层还需要 M(k - 1, N - 1) 次
  2. 如果没碎，在 (k, T) 之间，找出临界楼层还需要 M(T - k, N) 次

考虑最坏情况，在 k 层开始扔，两种情况需要取次数较多的一种，加上在第 k 层的一次，即

Mk(T, N) = Max{ M(k - 1, N - 1), M(T - k, N) } + 1

那么，对于 k 而言，可以是 1 到 T 层中的任意一层，所以对应 M 的值有以下选择

k 1 2 3 … T
M M1 M2 M3 … MT

根据题意，我们所求的 M，就是在 k 取[1,T]之间所对应的[M1,MT]中的最小值，即

M(T, N) = Min{ M1, M2, M3, …, MT }

那么，根据这个思路，就可以写出如下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
static int LeastTimes(int floor, int egg)
{
    if (floor < 1)
    {
        return 0;//一层都没有，不用扔蛋
    }
    else if (floor == 1)
    {
        return 1;//只有一层楼，只需要仍一次
    }
    else if (egg == 1)
    {
        return floor;//只有一个蛋，只能从一楼扔起，一个一个试
    }
    else
    {
        int result = int.MaxValue;
        for (int k = 1; k <= floor; k++)//选取k楼从1到T全部试一次，选取最小值
        {
            var Mk = Math.Max(LeastTimes(k - 1, egg - 1), LeastTimes(floor - kegg)) + 1;//碎没碎都有可能，运气差，取较大的
            result = Math.Min(result, Mk);//记录最小值
        }
        return result;
    }
}

问题小结

代码：HT.Algorithm的 EggDrop

顺着李老师的思路，这类问题应该不难理解，虽然我在大学里始终参不透玄机。

同款问题在LeetCodeCN-887. 鸡蛋掉落，很显然你不能直接用上面的算法妄想去 AC，脑补一下时间复杂度，应该是过不了任何一家 OJ 的。

鳄鱼小岛（与本文无关）

李老师留的课后习题，一并写了吧。网上也有说猫捉老鼠。

问题描述

李永乐老师：假如有一个圆形的小岛，然后有一条鳄鱼在圆形小岛周围游弋，鳄鱼的速度是人的四倍，而且鳄鱼总是希望找到一个离人最近的位置，而这个人最开始在这个小岛的正中心，那么我问这个人该如何运动，才能够比鳄鱼先到达这个岛的边缘，从而逃离这个岛呢？

解题思路

先做些设定，这个岛的半径为 r 米，人的速度为 v 米/秒，那么鳄鱼的速度为 4v 米/秒。

假设我就是那个被鳄鱼困在岛上的倒霉蛋，站在圆心，鳄鱼在正南方。

  1. 我想往正南方跑，那么我需要 r/v 秒的时间才能到，鳄鱼只需要 (πr)/(4v) 秒，很显然鳄鱼比我快，这样跑是不行的

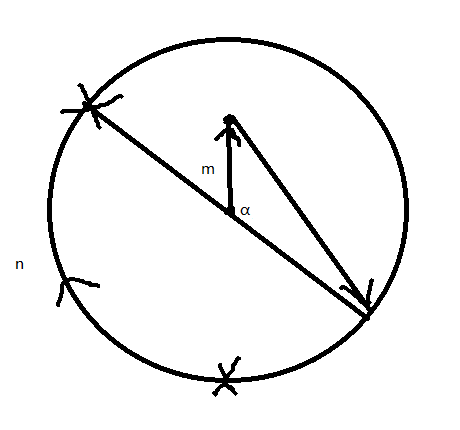
  2. 冷静想一下，根据题意，鳄鱼一定会选择劣弧，我沿着半径直线跑不行，那我始终沿着距离鳄鱼最远的点跑吧，也就是说，我需要更换我的目标点，这个点使得鳄鱼必须要再跑 πr 的路程

  3. 假设我更换目标点时，我已经跑了 m 米远，鳄鱼跑了 n 米远，我因为目的地转换而产生的圆心角为 α ,那么很显然，当 α ≥ π/4 时，我接下来要跑的路程比半径还远，鳄鱼一定比我快

  1. 那么，换个思路想，是否存在一个角度，这个角度可以使得我沿半径方向在逐步靠近边缘，而始终让鳄鱼需要再走 πr 的距离，也就是，我和圆心和鳄鱼共线在同一条直径上

  2. 很容易想到，在同一个圆心，半径为 r/4 的圆里，我是完全办得到的，因为在这个圆里，即便鳄鱼的速度是我的四倍，我跑的角速度也是大于或等于鳄鱼的角速度，使得三点共线

  3. 那么，在我跑到 r/4 处，只要沿着圆心相反的方向再跑 (3r)/4 的距离就可以跑到边缘，对于我而言，我所需要的时间是 (3r)/(4v) 秒，而鳄鱼需要 (πr)/(4v) 秒，显然我更快，那么我就成功逃离了

问题小结

这道题，算数学问题还是算物理问题呢？

后记

用递归的方法去解决问题，代码看起来很优雅，但到了像比较复杂的动态规划里，普通递归的代码就带来肉眼可见的时空间复杂度，这往往是不可接受的。

对于学习理解来说，这种写法尚可，但在实际解决问题时，需要去做优化，这种优化有的是基于强大的数学功底，例如

有的则是记忆、剪枝等等，罢了，不说了，接着留坑吧。