相遇问题

发表于 分类于 阅读次数： 本文字数： 1.4k 阅读时长 ≈ 1 分钟

前言

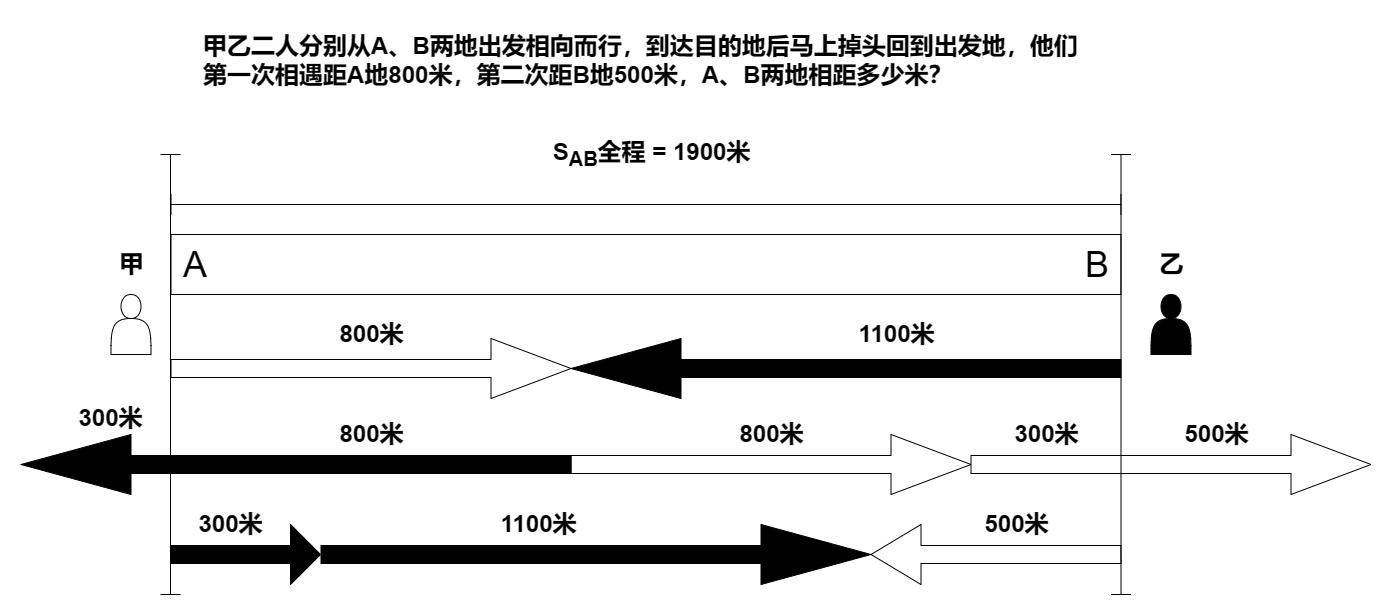
甲乙二人分别从A、B两地出发相向而行，到达目的地后马上掉头回到出发地，他们第一次相遇距A地800米，第二次距B地500米，A、B两地相距多少米？

分析

毫无疑问，两人在两地相向而行，第一次相遇肯定是在AB两地之间，且两人一共走完了一个全程的距离。

显而易见，问题就是第二次相遇，第二次相遇究竟是什么情况，脑补一下，两人在第一次相遇后继续前行，走得快的那一位先到达目的地，走得慢的那一位后到达目的地，两人都会掉头继续相向而行，于是有了第二次的相遇。

既然两人掉头后有了第二次的相遇，那么也很容易想到，第一次相遇与第二次相遇之间，两人一共走完了两个全程的距离。

接着往下想，第二次相遇与第三次相遇之间，两人也是一共走完了两个全程的距离。

那么，可以做个简单的推论，只有第一次相遇，两人走完了一个全程，而后的每次相遇，两人都走完了两个全程。

也就第n次相遇，两人一共走了2n-1个全程的距离。

解

如果可以想通到第二次相遇时，两人一共走了三个全程的距离，那么很容易想到，甲既然第一次相遇走了800米，那么第二次相遇，应该走了800 x 3 = 2400米，而甲在第二次相遇时，应该走了一个全程加回头走的这500米。

所以，全程的距离就是800 x 3 - 500 = 1900米。我们可以画个草图验证一下。

盲点

人总是容易发现盲点，很容易想到，两人都掉头后才有的第二次相遇，是不是有些势均力敌了，有没有可能两人压根就力量悬殊呢，一方在还没有到达目的地时就已经被追上了呢，当然是有可能的。

但这就需要讨论一下相遇的定义了，在数学问题分类里，关于行程类的问题，是有相遇问题和追及问题这两类的。所以，这个盲点其实是在说，“相遇”的情况我们讨论完了，那“追及”的情况是不是属于这道题的范畴了。

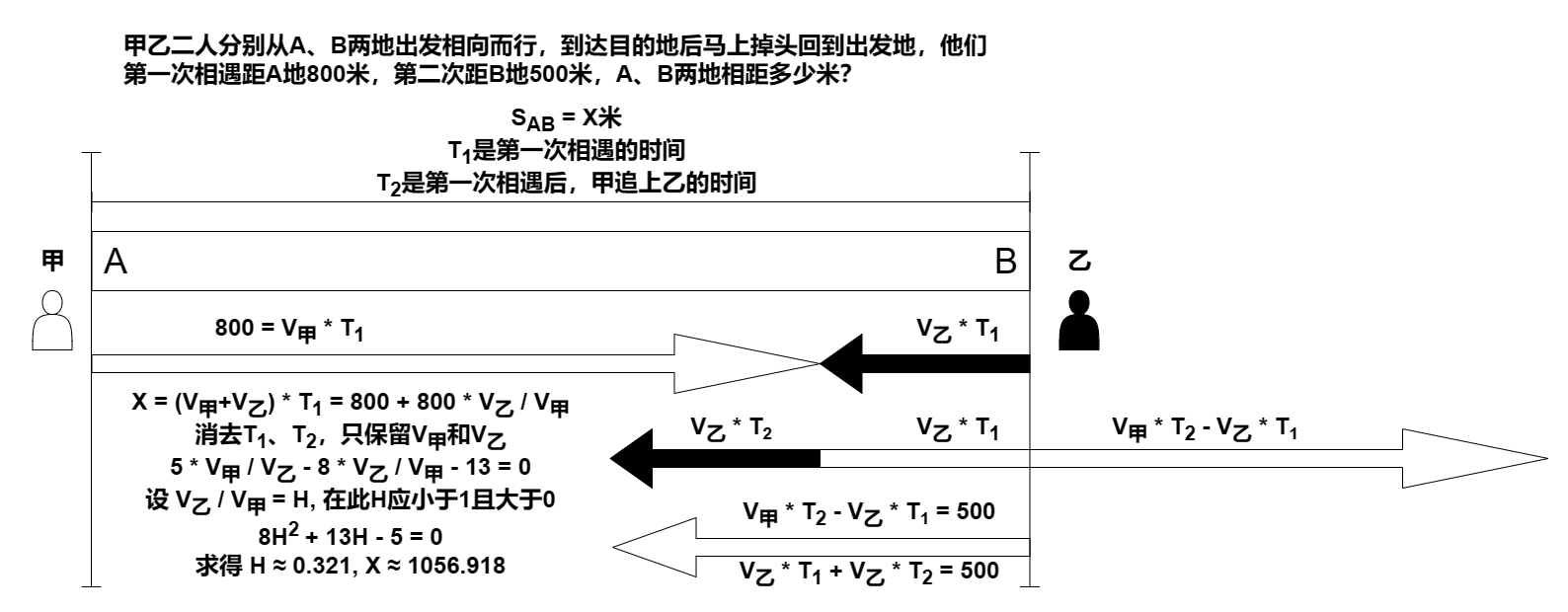
甲比乙快得多

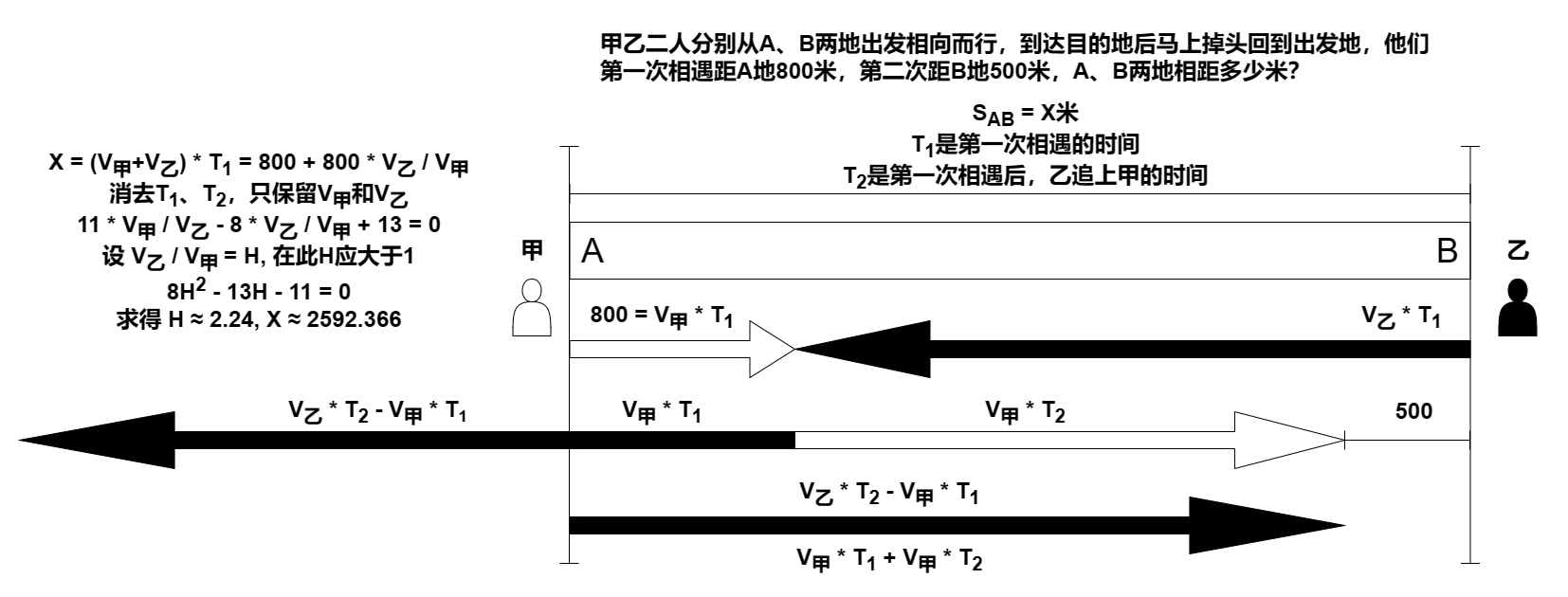
乙比甲快得多

追及问题

按照题目给的数据，在追及的情况下，算出来的结果不太舒服吧，那我们能不能自己构造一些数据，重新设计一下题目，从而获得一些令人舒适的数字。

经过上面的计算发现，我们总是选择消去时间，因为两人所耗费的时间总是相同的，很好理解吧，真正的变量其实只是全程的距离S米，以及两人的速度比值H（借用上面的假设，H = V乙 / V甲）。

假设第一次相遇耗费的时间是T1，那么

1
S = (1 + H) * T1

假设第一次相遇后，直到第二次相遇，耗费的时间是T2。

甲比乙快得多

1
2
3
4
5
6
7
V甲 * T2 - V乙 * T1 = V乙 * T1 + V乙 * T2
等式两边除以V甲
T2 - H * T1 = H * T1 + H * T2
T2 * (1 - H) = T1 * 2 * H
T2 / T1 = 2 * H / (1 - H)
很容易想到 H = 1/3 时，有整数的比例
也就是甲的速度是乙的三倍

于是可以这样构造

  • AB两地相距12米
  • 甲的速度是9米/秒
  • 乙的速度是3米/秒
  • 第一次相遇，距离A地9米，距离B地3米，耗时1秒
  • 第二次相遇，距离A地6米，距离B地6米，耗时1秒
  • 总共耗时2秒

乙比甲快得多

1
2
3
4
5
6
7
V乙 * T2 - V甲 * T1 = V甲 * T1 + V甲 * T2
等式两边除以V甲
H * T2 - T1 = T1 + T2
T2 * (H - 1) = T1 * 2
T2 / T1 = 2 / (H - 1)
很容易想到 H = 3 时，有整数的比例
也就是乙的速度是甲的三倍

于是可以这样构造

  • AB两地相距12米
  • 甲的速度是3米/秒
  • 乙的速度是9米/秒
  • 第一次相遇，距离A地3米，距离B地9米，耗时1秒
  • 第二次相遇，距离A地6米，距离B地6米，耗时1秒
  • 总共耗时2秒

后记